IsometricProjection

2000-01-01

Isometric projection

Wikipedia says this: http://en.wikipedia.org/wiki/Isometric_projection
So, it can mean a projection where all 3 directions are projected to the same length, i.e. they meet at exactly 120°.
Here, I don't mean this "true" isometric projection, but one which is close (but really a dimetric projection), and nice to be used in pixel games. It is the projection where a square tile viewed from above has exactly a ratio of 2:1 - so it means, when doing pixel art, a straight line along a floor axis is 2 by 1 pixels.

An isometric map

Rotated diamond

If you want to deal with an isometric game, there's of course several ways. One common way is to use a standard tilemap, and sort of rotate it by 45°. In the following, I assume it is rotated 45° degree clockwise - so the new origin lies at the top.

So, our map is now diamond shaped. The origin is at the top, the x-axis goes right down, the y-axis left down. Of course, it works just as well if you put the origin left, and let the x-axis go right up, and the y-axis right down. I just like my game objects to be at the top of a tile when its position is 0/0, instead of at the left.
What is important is, internally, our game need not know about the isometric display. It just sees a normal tilemap like to the left - only the display is different.
Before delfing further, let's see how exactly an isometric tile can be displayed now. Assume, we want to draw the tile at x/y. So in the picture e.g. 0/0 would be the topmost tile, and 0/3 the leftmost one.
The tile 0/0 of course would be drawn at pixel position 0/0 (if we just set the top of the diamond as 0/0 on screen). And the leftmost tile would be drawn on (3 * w * -0.5 / 3 * h * 0.5), so in our example (-48/24). w/h are the width and height of a single diamond shaped tile, the picture uses 32x16 tiles. In general, the tile on tile_x/tile_y is drawn on:

pixel_x = tile_x * tile_w/2 - tile_y * tile_w/2
pixel_y = tile_x * tile_h/2 + tile_y * tile_h/2

This transformation can be put into a function isometric_transform, and then the code to draw our tilemap gets very simple:

for each tile_x, tile_y:
    pixel_x, pixel_y = isometric_transform(tile_x, tile_y)
    picture = map.get_picture_at(tile_x, tile_y)
    picture.draw(pixel_x, pixel_y)

In words, for each tile in our map, get the corresponding pixel position, and draw the tile there.

Inverse mapping

Now, we basically are done for simple games. We can now put all sorts of stuff into our tilemap, and deal with it as if it was a non-isometric map. But if the game is e.g. isometric minesweeper, there is a problem: When the mouse is clicked over our map, which tiles was it over?
Myself, I best like to simply build the inverse of the formula above, and then get back two floating point numbers, where the integer part tells me which isometric tile a pixel position is in, and the fractional part tells me where in the tile it is (the latter can simply be discarded if it is not needed).
The formulas are:

tile_x = (pixel_x/(tile_w/2) + pixel_y/(tile_h/2)) / 2
tile_y = (pixel_y/(tile_h/2) - pixel_x/(tile_w/2)) / 2

For example, if in our example 4x4 map at the top, the mouse is clicked on pixel position 20/40 - which tile is there? The size of the tiles is 32x16. So we get:

tile_x = (20/16 + 40/8) / 2 = 3.125
tile_y = (40/8 - 20/16) / 2 = 1.875

So, the tile is 3/1, and we even know that it is at (.125/.875) inside the tile. .0/.0 would mean the pixel is exactly the topmost pixel inside the tile, .99/.99 would mean it is at the bottommost pixel.
Pixel -48/24 from the initial example would accordingly yield the tile position ((-48/16+24/8)/2,(24/8-(-48/16))/2) or (0.0/3.0).

Pixel positions

By now, we can make a complete isometric minesweeper, or any other game using 2D gameplay and an isometric display. To draw a tile, we transform to isometric pixel coordinates, and if we need to find a tile at some screen position, we can transform back to tile coordinates.
But what if we have other stuff on our tiles than just a single tile picture? Houses, trees, little people, or whatever else. We can just put them on their tile so far, but what if such a game unit wants to smoothly travel from one tile to the next?

• There are different possibilities now. Such units could for example use a normal, not transformed offset position inside the tile. With our sample 32x16 tiles, they could e.g. roam inside a diamond with the four corners (0/0), (16, 8), (-16, 8), (0, 16).

• Another possibility would be to make the units completely independent of the tilemap, keep their position in normal, un-transformed pixel coordinates, and use our second transform above to convert into fractional tile coordinates for drawing them.

• The first two solution both do something bad though: They mix up different coordinate system, which in a somewhat bigger game will sooner or later cause you to scream at your code. I prefer to keep the fact of an isometric display confined to the drawing code, and to things like mouse positions. An easy way for this is to keep the intra-tile positions of objects in the floating point rectangle 0/0 to 1/1, that is, in the same fractional positions we already have in the pixel-to-tile transformation. So if for example there's a tree on tile 2/2 and it is on 0.5/0 inside that tile, we know that tile is drawn at (0,32). More precisely, its topmost pixel is at (0,32). Now, the intra-tile position can be transformed with the same formula, and (0.5/0) is (8,4). So we can added that offset in pixels to draw the tree there.

• If each tile of the game stores its objects, then probably the previous method is best. But instead of using intra-tile positions, it can sometimes be better to store global coordinates for units. In this case, our tree would then be at 2.5/2. And the transformation formula still works, and returns (8,36). (At least, as long as floating point is used.)

There are of course other ways, especially in original old games the formulas will be adjusted to work with integer only. But I do like my way a lot. All I need are the two initial transformations, from tile-to-pixel, and from pixel-to-tile. And using floating point, this always works, for tile positions, intra-tile positions, and it even works out for sub-pixel accuracy if you are using all normalized coordinates, e.g. when using OpenGL. And the advantage, the game logic never needs to know that the display is isometric. All my coordinates (tile as well as intra-tile, or global coordinates) are just normal 2D coordinates for a non-isometric map. Only the two transformations transform to and from screen coordinates.

Pixel art

Our projection is welcome to pixel artists, because you can pixel straight lines simply by using 2 pixels in the x direction for every pixel in the y direction. It can look very nice, since it allows you to draw very exact geometry. The below picture can help understand where exactly pixels go - in the example tiles are only 8 pixels wide - but it works the same for bigger ones of course.

Of course, the angle between the edges is not 120°, and also the third dimension, the up-direction, must have a different length to produce something looking like a cube. The projection to get 2:1 lines is one where you look down on the floor by an angle of exactly 30° (2:1 lines itself have an angle of about 26.565 though, don't confuse those angles.)
Here an old ASCII art explaining how to get to the 30°, but it's not important:

  \     / view vector
    \ /
    /.\  l/2
  /     \
/_________\
 a     l    \ view plane

At the bottom, there's the tile, with length l. It is viewed from an angle a, and
 we want it to appear as length l/2 (the vertical direction in the pixel art). The sideways direction (horizontal in the pixel art) will continue to be l, so the result will be the desired - lines who are exactly 2:1. This means:

sin a = 1/2 -> a = asin 1/2 = 30°

So, the angle to the floor should be exactly 30° (and conversely, the angle to the vertical should be 60°).

Height

Now, the interesting thing for us is only, how many pixels high must something be drawn to be as long as the side of an isometric tile?
First, again a quote from the same old (and hard to understand, especially as I only quote some small parts) ASCII art aticle: What about height?

  |\
h'| \h
  |  \
  |   \ 60°
  ------

If something has a height h, what will be the projected height h'?
We know h' / h = sin 60° = cos 30° = sqrt(3) / 2. So if something is h' pixels tall, it
really is h = h' * 2 / sqrt(3) pixels high. And if we want something to have a height of h,
we draw it as h * sqrt(3) / 2 pixels. Real height to drawn pixels is 2 to sqrt(3).

Turning everything by 45°, we get this:

  /\
 /  \
 \  / |
  \/s | x / 2
 __x

2 * x^2 = s^2
 s = x*sqrt(2)

A diamond.

To make the width x units, the side length must be x*sqrt(2);

Now, what it means, is this. We have an isometric tile, which let's say fits into a 64x32 rectangle. So the 'x' in this case is 32. This means, a side really (un-projected) has a length of s = 32 * sqrt(2). And we know by the formula above that something appearing x pixels high really is 2 * x / sqrt(3). So: 32 * sqrt(2) = 2 * x / sqrt(3), or x = 16 * sqrt(2) * sqrt(3). Believe it or not, as always with math formulas, but the result would be about: 39.192
There's no need to understand any of this, just know: For an isometric tile which fits into 64x32, make something 39 pixels tall to have about the same height as a side is long.

This cube also will align exactly when using in an isometric tile-map, or stack on top of others. All you need to remember is, if your tile fits into a box w * h (where w = 2 * h, e.g. 64 * 32), then (h * sqrt(6) / 2) is how many pixels high to get a perfect cube.
In summary (x is horizontal, y is vertical, z is depth):

• z / x = 1 : 2
• z / y = 1 : sqrt(3)

3D Models

Where this really is relevant is if you want to project a 3D model to fit the pixel art. By modelling a cube, then viewing it from exactly 30° from above, and from 45° from the side, and using orthographic projection, you should get something like this cube. It's also a good way to verify the formula.
Actually, here's an example done in Blender (for something else, but still). Also a version without subsampling.

Sorting

So far, everything is very nice. We have a tilemap, we can choose how we want object positions mapped into the map, and we know how to draw our objects (if we would have any artist skills at least).
But how can we properly draw objects? Looking at the tilemap, it is simple. If we draw from top to bottom, row-wise (in display rows), we should be all sets. There can now be boxes, columns, whatever standing on the tiles, and it still will look alright. Even if e.g. those trees overlap - they are drawn in the right order.
(insert picture with some columns)
But, if we would now try adding a sprite and moving it between those columns-tiles, it would not work out easily. The sprite could be drawn along with the tile it is standing on - but what if it moves between tiles? One idea which works is splitting each moving sprite into halves, one for each tile it is on. This is relatively easy to do, and works all right for simple cases. E.g. in a diablo1 style map, we should be all set. Whenever the player or a monster moves around a corner, internally there will be two halves, one still on the tile behind, the other in front.
(insert picture from Feud)
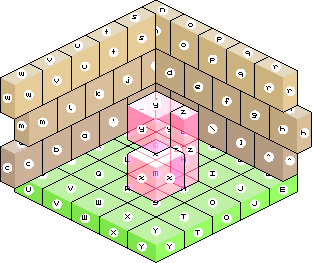
But, what in the general case? Like, we want to also move on top and below objects? We want to stack up boxes and push them around? Before looking for an answer, here a picture:

In which order would you sort the three boxes?
Well, now, it makes a whole lot more sense that we actually did split our blocks before, instead of looking for a better way to sort them. Since, in fact, you cannot sort isometric objects (or 3D objects in general, for that matter).
This is of a course a rather big problem for anyone attempting to create an isometric game. Sorting still may be the best option. For example, if we sort by distance of the object center to the viewer, it will work good enough, if the objects don't come too close.

Splintering

But what if we want to draw those three boxes correctly? A single split along one of the cubes apparently makes it work. So maybe we can come up with a splitting rule like with the player-walking-between-columns before?
My endeavors in that direction so far led to some interesting non-polynomial-time splitting algorithms. What that means is, just comparing each object to each other is not enough, instead i end up with even more checks for a possible split. For few objects this doesn't really matter, and there's a lot of optimization potential as distinct groups of objects which are not overlapped could be singled out. However, the complexity for the engine just is bad.. instead of isometric objects each consisting of an image, i have now a collection of object splinters for each object.

Z-buffer

So, why don't we go for the classic solution: A z-buffer. This means, we can't simply use one single picture for our 3d objects, but need depth information. E.g. a box could consist of 3 planes for left/right/top side.
So, if not using pixel art, this of course is the natural choice. But there's a trick we can use for classic isometric sprites. If we have width/height/depth for our isometric sprite, we create a 3D cube with those dimensions and display each isometric object as such a cube, with a projection as described earlier. Each cube has three visible faces. We now set the texture coordinates for each phase to their actual display coordinates (they are easy to calculate), and in this way 'pin' the flat 2D-sprites on top of the 3D-cubes. The result is that the z-buffer does all the per-pixel sorting for us. We only need to make sure that the 3D cube is big enough to cover the whole sprite or parts may get cut off.
Of course, if there are transparent objects, this runs now into all the problems usually associated with transparency and the z-buffer. There are two things to look out for - completely transparent pixels, and partly translucent pixels.
For the former, the way z-buffers work is usually to not update the buffer for such pixels. This is very important for isometric sprites - as except for some cases like a brick wall, objects will not at all have the shape of an isometric cube but contain a lot of transparent pixels. In fact, it usually will not be possible to have the collision box and render box coincide, so the actually drawn isometric cubes will overlap. If one of your isometric characters has for example long floating hair, expect the hair to get clipped when near a wall. Usually not a big issue.
If your game needs translucent objects, things get more problematic. If there's only a few of them, like an occasional glass wall, one trick is to defer rendering until everything else is rendered. The zbuffer (for all solid objects) will be fully set up. If now a translucent object is rendered, it will let the things behind it shine through correctly. This doesn't work if there are multiple translucent objects though. However, sorting the translucent objects and drawing them in order (without updating the z-buffer) should usually work fine. A case like the 3 cubes earlier will look wrong if the cubes are translucent - but usually also not a big issue.

Masking

This is a solution when someone told me about I couldn't believe I hadn't thought of it earlier. It's likely how early isometric games actually were implemented. The idea is very simple.
For each isometric object to be drawn, we check if it will be drawn overlapping any already drawn object which actually should be in front of it. If so, we create a mask (using e.g. the stencil buffer or the depth buffer). The mask is completely opaque first not cutting away anything. Then we draw all the overlapping objects we just found into it, setting each pixel to masked. So our mask/stencil is a binary bitmap now, which has 1s everywhere, but 0s wherever there are pixels of any of those objects. Then we draw our object we are just drawing, using the mask (only pixels where the mask is 1 are drawn).
It's easy to see why this will always work. The key is that for just two objects, there is no problem. If there are only 2 isometric objects, we always can get a perfect result by simply drawing the one behind first, then the other one in front. In the above algorithm, we know we have a flawless scene (initially completely empty). If we draw our new object, the only way we could introduce a mistake is by drawing over other objects which are behind. So we mask out all pixels belonging to such objects - problem solved.
For translucent objects, when the object is drawn we know that all objects which are not yet drawn but have overlapping pixels which are behind it would end up wrong. So an idea would be to get a list of those objects, then create a mask with all pixels of our object. Then we draw those objects using the mask (they have to be sorted somehow though). After that we draw our translucent object like before, using another mask to not overdraw anything already drawn but in front. Unlike the z-buffer solution, this gets our 3-cubes example perfectly right even if they are all translucent. However, as we know there is no good way of sorting isometric cubes, a solution working in all cases involving translucent objects would likely require a recursive algorithm instead of simply sorting. If there's not a lot of translucent objects just drawing all opaque ones first and then the translucent ones should work well enough. The problems here are the same as with general 3D now.
Here's a screenshot from my isometric engine which simply draws the translucent objects at the end: